Visualisation de graphe

Le graphe est un objet mathématique permettant de décrire des systèmes de nature très différente comme la circulation sur un réseau routier, les interactions sociales, la connexion de neurones dans un cerveau, ou les citations d'articles scientifiques, notamment dans le cadre de la théorie des réseaux. Dans cet article de blog, je propose un aperçu illustré du sujet et introduis la notion de visualisation d'un graphe.

Quelques exemples

Les neurones du cerveau de poisson zèbre

En exprimant une molécule fluorescente dans un seul neurone du cerveau, on peut tracer la trajectoire d'un neurone dans toute sa longueur : position du soma et prolongement de l'axone. Cela permet de faire des cartes de connectivité du cerveau pour mieux comprendre son organisation topologique.

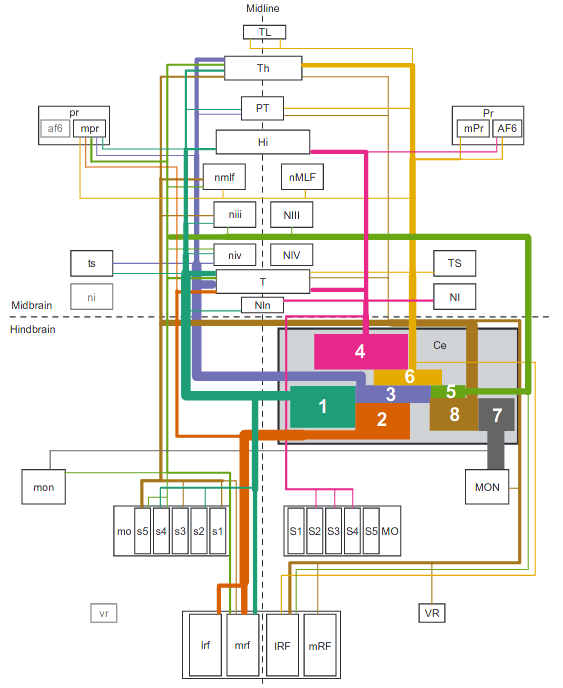
(gauche) schéma du graphe du cerveau (DOI, supplementaries) (droite) neurones oculomoteurs et leurs projections, réalisé sur https://fishatlas.neuro.mpg.de/

Les routes dans la ville du Havre

Si l'on considère chaque carrefour comme un point, on peut regarder comment ils sont connectés via des routes. Chaque connexion peut avoir des caractéristiques comme la vitesse maximale, le type de voie... Les algorithmes d'itinéraires opèrent sur le graphe constitué de ces connexions !

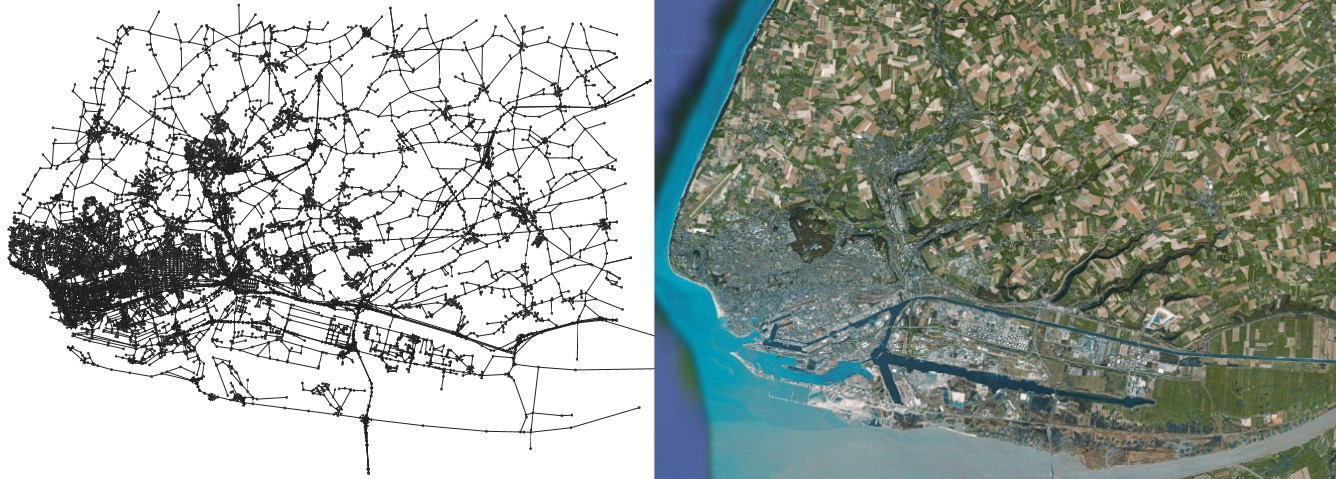
Graphe des liaisons routières dans la ville du Havre produit par https://graphstream-project.org/doc/Tutorials/Graph-Visualisation/

Les citations de publications scientifiques

Dans les exemples précédents, les graphes représentaient des données spatialisées en 3D (neurones) et 2D (routes) Mais quand il s'agit de publications scientifiques, comment produire une visualisation spatiale de la connaissance ? En étudiant la manière dont les articles se citent, on peut définir une notion de proximité et ainsi produire une représentation.

Exemple d'article scientifique (DOI) et visualisation des citations produite par https://www.connectedpapers.com/

Spatialisation par simulation de forces

Une famille d'algorithmes de spatialisation qui m'intéresse pour sa simplicité et sa flexibilité est la simulation de forces physiques (https://en.wikipedia.org/wiki/Force-directed_graph_drawing). L'idée générale est de définir des règles locales qui correspondent à ce que l'on veut observer à l'échelle globale. Par exemple, si l'on veut que deux noeuds connectés par un lien apparaissent plus près l'un de l'autre que deux noeuds non connectés, on simule les liens comme des petits ressorts attractifs et les noeuds comme des aimants répulsifs.

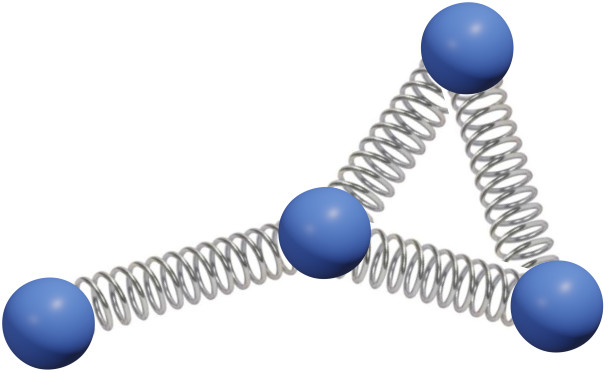
(gauche) schéma de boules reliées par des ressorts (droite) simulation dans le navigateur, les boules peuvent être déplacées à la souris

Un des avantages de cette méthode est qu'elle permet de réagir dynamiquement à une éventuelle évolution du graphe. C'est cette propriété que j'ai utilisée pour illustrer la toile de confiance de la monnaie libre ğ1 tout au long de son histoire :

Historique de la toile de confiance de la ğ1. Plus de détails sur peertube. Chaque identité est représentée par un disque bleu de diamètre proportionnel au nombre de certifications actives reçues. Une certification est représentée par un segment de droite en gris clair.

Ces méthodes de spatialisation permettent de se représenter un graphe à condition qu'il soit suffisamment petit et peu dense (nombre de lien petit devant le nombre de liens possibles), mais sont difficilement lisible dans le cas contraire. On peut alors s'orienter vers des outils d'exploration interactifs ou compléter la visualisation par des détections de communautés ou des données complémentaires facilitant la spatialisation.

J'espère trouver du temps prochainement pour rentrer vraiment dans le sujet suite à cette introduction très superficielle !